Part 1 Part 2 Part 3 Part 4 Part 5 Part 6

 Sudoku Course:    

Welcome to Course in Sudoku

Part 2

‘Locked’ Candidate Reduction Method

To solve a sudoku puzzle you need to fill each empty square with one of the digits 1 to 9 so that each digit occurs only once in each row, column and box.

Sometimes it may be difficult to place the correct digit in some of the squares. There are just too many possibilities. In that case the number of candidates needs to be reduced. To do that you need to see the candidate table.

The Sudoku Instructions Program can calculate and display the candidate table at each stage in the solving process, so you can see the possible digits in each square of the Sudoku board.

To reduce the number of candidates you study the candidate table closely to find candidates, which may be removed from the squares. This is done using pure logic. There are various methods to apply.

In this part of the course we will describe a relatively easy method called the ‘locked’ candidate method. To use this method you need to look at

A) the rows and columns passing through each box

or

B) each box and the rows and columns passing through it.

This may seem the same, but it is not quite the same - the starting point is different. The following four different situations will clarify the method.

A1) Row - Box

Look at rows to see if a candidate digit is confined to a single box.

If this is the case the candidate digit is 'locked' inside that box. Since the box can only have this digit once, that candidate digit can be removed from the other rows within that box.

Here you can see that within row 3 candidate digit 7 occurs only inside box K (blue digits). So, within box K digit 7 is ‘locked’ in row 3. Therefore candidate digit 7 can be deleted in other rows within box K (red digits).

At this stage we only know that 7 should be in either square E3 or F3. The exact location of 7 in row 3 will become clear later in the solving process.

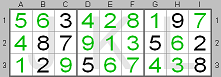Here you can see the final solution for this part of the board. In row 3 digit 7 should be in square F3.

A2) Column - Box

Look at columns to see if a candidate digit is confined to a single box.

If in a column a candidate digit is confined to a single box, it is ‘locked’ inside the box. Since the box can only have this digit once, that candidate digit can be removed from the other columns within that box.

Here you can see that within column C candidate digit 1 only occurs inside box P (blue digits). So, within box P digit 1 is ‘locked’ in column C. Therefore, candidate digit 1 can be deleted in other columns within box P (red digits).

At this stage we only know that 1 should be in either square C8 or C9. The exact location will become clear later in the solving process.

In this smaller picture you can see the final solution for this part of the board. Within box P digit 1 should be in square C9.

B1) Box - Row

Look at boxes to see if a candidate digit is confined to a single row.

If within a box a candidate digit is confined to one row, it is 'locked' in that row. Since the digit can occur only once in the row, that candidate digit can be removed from that row outside the box.

Here you can see that within box K candidate digit 1 only occurs in row 1 (blue digits) - it is 'locked' in row 1. Therefore, outside box K candidate digit 1 can be deleted in row 1 (red digits).

At this stage we only know that 1 should be in either square E1 or F1. The exact location will become clear later in the solving process.

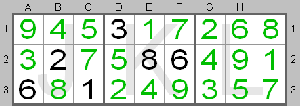Here you can see the final solution for this part of the board. Within box K digit 1 should be in square E1.

B2) Box - Column

Look at boxes to see if a candidate digit is confined to a single column.

If a candidate digit in a box is confined to one column, it is 'locked' in that column. Since the digit can occur only once in that column, that candidate digit can be removed from the column outside the box.

Here you can see that within box P candidate digit 7 only occurs in column A (blue digits) - it is 'locked' in column A. Therefore, in column A candidate digit 7 can be deleted outside box P (red digits).

At this stage we only know that 7 should be in either square A7 or A8. The exact location will become clear later in the solving process.

In this smaller picture you can see the final solution for this part of the board. Within box P digit 7 should be in square A8.

By repeating finding ‘locked’ candidates in the sudoku puzzle, the number of candidates can be reduced considerably.

This relatively simple candidate reduction method can make difficult sudoku puzzles easier to solve. The Sudoku Instructions Program can help you locate ’locked’ candidates as shown in this part of the course.

In the beginning you can let the program find the ’locked’ candidates and get the program to do the candidate removal.

Later when you get more experience you can also - using the program - find the ’locked’ candidates yourself and perform candidate removal yourself. The program permits doing it either way.

In the next parts of the sudoku course we will present other important candidate reduction methods.

Happy Sudoku Solving!

© Sudoku Instructions Programming Unit - All rights reserved