Sudoku Course:
Welcome to Course in Sudoku
Part 3
Naked Candidates Reduction Method
In this part of the course we will present another method to reduce the number of candidate digits to better solve the puzzle. For this we need the candidate table as displayed by the Sudoku Instructions Program.
The method for candidate reduction that we present is based on finding naked candidates. Candidates are ’naked’ if they are alone, that is not ’hidden’ among other candidates in a square.
If you have just one candidate in a square you have a naked or isolated single (see part 1). You can just place that digit in the square.
However, if you have naked candidates in pairs, triples or quads, you will be able to use them to perform candidate reduction. Again this method is based on pure logic.
If naked candidates are present these candidate digits must necessarily be in the squares in question. Therefore, these candidate digits can be removed the other squares within the same group (row, column or box).
In the squares with ‘naked’ candidates we do not yet know the exact position of each digit, only that they collectively should be in those squares.
Later in the solving process the unique position of each digit will become clear. We will go through the naked candidates method for pairs, triples and quads and give some examples. For this purpose we will use the candidate table as displayed by the Sudoku Instructions Program.
Naked Pairs
If two squares in a group (row, column or box) have the same pair of candidate digits and only these, then these candidates make up a ‘naked’ pair. The two digits are linked to those two squares. Therefore, those candidate digits can be removed from the other squares within the group.
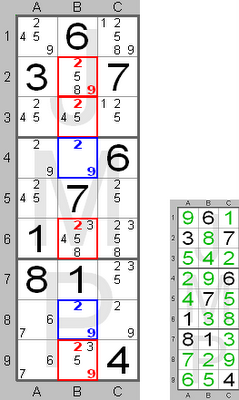This board shows a 'naked' pair (2 and 9) in column B (blue digits). These candidates
are 'naked' because no other candidates are present in those squares. Those digits
are therefore linked to those squares. The candidate digits, which can be removed
from the other squares in column B, are shown in red.
In the small picture you can see the final solution for this part of the board. In column B digit 9 should be in square B4 and digit 2 in square B8.
Naked Triples
If in three squares within a group the candidates are limited to three digits, those candidates make up ‘naked’ triples. Those digits are linked to the three squares. Therefore those three candidate digits can be removed from the other squares within the group. All three candidate digits need not be present in all three squares.
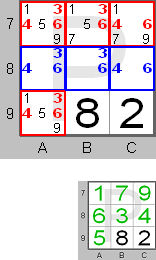This board shows 'naked' triples (3, 4, and 6) shown with blue digits. These candidates
are 'naked' because no other candidates are present in those squares. The digits
are therefore linked to those squares. The candidates, which can be removed from
the other squares, are shown in red.
In the small picture you can see the final solution for this part of the board. In box P digit 6 should be in square A8, digit 3 in square B8 and 4 in square C8.
Naked Quads
If in four squares within a group the candidates are limited to four digits those candidates make up ‘naked’ quads. All four candidate digits need not be present in all four squares, but those digits are linked to the four squares. Therefore those four candidate digits can be removed from the other squares within the group.
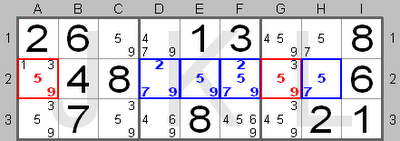
This board shows 'naked' quads (2, 5, 7 and 9) shown in blue in row 2. These candidates are called 'naked' because no other candidates are present in those squares. The candidates, which can be removed from the other squares are shown in red.
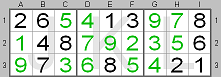In this picture you can see the final solution for this part of the board. In row
2 digit 7 should be in square D2, digit 9 in square E2, digit 2 in square F2 and
digit 5 in square H2.
This method of finding ‘naked’ candidates in Sudoku can be used repeatedly to reduce the number of candidate digits. Thereby the full solution of the Sudoku puzzle may be easier to obtain. This relatively simple candidate reduction method can make difficult sudoku puzzles easier to solve.
The Sudoku Instructions Program can help you locate hidden candidates as shown part of the course.
In the beginning you can let the program find the ’naked’ candidates and get the program to do the candidate removal.
Later, when you get more experience, you can also -
In the next parts of the sudoku course we will present other important candidate reduction methods.
Happy Sudoku Solving!
© Sudoku Instructions Programming Unit -